Our research and development focuses on a pioneering 3D Artificial Intelligence Model, leveraging cutting-edge technologies such as Convolutional Neural Networks (CNNs), Graph Convolutional Networks (GCNs), Transformers, and Physics-Informed Neural Networks (PINNs) to achieve breakthroughs in 3D understanding.
Convolutional Neural Networks (CNNs) are often used in AI models that recognize images using deep learning technology.
This is because the amount of image data is large and it is difficult to calculate with a neural network unless it is compressed using CNN convolution and pooling processing.
The simple example below illustrates the procedure by which an image of 32 times 32, 1024 pixels is compressed into a 20-dimensional fully connected layer.

Two-dimensional image convolution uses an array of pixels. Since the arrangement of pixels is fixed as shown in the figure below, it is possible to convolve with a filter of fixed shape and size.

The 3D shape recognition technology that we are researching and developing also requires the convolution technology as well as the 2D image.
A 3D shape is a 3D geometry created by a 3D CAD or 3D scanner.

Before the spread of 3D CAD, design data was two-dimensional drawing data, but now design data is stored as a three-dimensional shape with three dimensions of height, width, and depth, and is used for various purposes.
These three-dimensional shapes are data that have X, Y, and Z coordinate values at each node (vertex) position.

By understanding the node position and the connection between the nodes, AI can recognize the features and dimensions of the shape.
3D shape convolution technology is used in the process of recognition by 3D AI.
Looking at the 3D shape data mentioned above in detail, the number of internode networks is not fixed as shown in the figure below, so the same fixed size filter as the 2D image cannot be used.
Our technology allows us to convolve this variable network structure, which allows AI to efficiently recognize 3D shapes.

Graph Convolutional Networks (GCNs) differ from traditional Convolutional Neural Networks (CNNs) in that they adapt the convolution operation to work on the irregular structure of graphs, rather than processing information on a fixed grid.
Unlike general Graph Neural Networks (GNNs), GCNs specifically leverage neighboring node information through a specialized convolution operation designed for graph data. This allows GCNs to effectively capture the relationships and dependencies in graph-structured data.
Feature Aggregation: GCNs aggregate information from neighboring nodes by combining the features of a node with the features of its immediate neighbors. This can be done through various methods, such as averaging, weighted summation, or more sophisticated attention mechanisms.
Feature Transformation: After aggregating neighbor information, GCNs apply a learnable transformation to the combined features. This transformation, often implemented as a simple linear layer, allows the network to learn complex relationships between a node and its neighbors.
Stacking Layers for Deeper Understanding: Like traditional CNNs, GCNs can be stacked in multiple layers. Each layer aggregates information from a wider neighborhood, enabling the network to capture higher-order relationships within the graph.
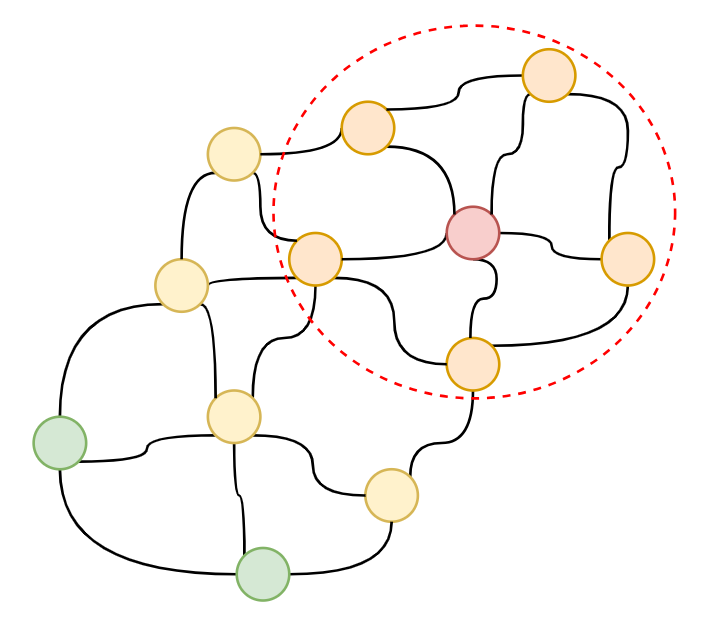
Classification is a major area where convolution is became a game changer, convolution in GCNs help capture local neighborhood information and propagate it through the graph, allowing nodes to “learn” from their surroundings, that makes it excel in Node Classification.
Convolutions, when combined with pooling, enable the network to learn a global representation of the graph’s structure, which is essential for classifying the entire graph. After multiple convolutional layers, a pooling operation (like global average pooling) can be used to aggregate the node-level representations into a single, fixed-size vector that represents the entire graph. This graph-level representation then be used for classification.
The developed 3D shape recognition AI model can be applied to functions such as classifying shapes into specified groups by recognizing their features, matching not only shapes but also dimensions, and synthesizing new shapes by mixing features of multiple shapes.

A Transformer is a type of neural network architecture that’s really good at understanding and working with sequences of data. Before Transformers, Recurrent Neural Networks (RNNs) like LSTMs and GRUs were the dominant architecture for processing sequential data (text, time series, points, etc). This makes it great for tasks like generative model, summarization text, translation and a lot others.
Transformer use something called “Attention”, it revolutionized sequence modeling with “Attention mechanism” that enabling parallel processing so make transformer faster and allows transformer to capture relationship between different parts of the sequence, even if they’re far apart.
Transformers often (not always) utilize an encoder-decoder architecture to train models depend on architecture purpose. Initially, the input is embedded into vectors that capture the essence and relationships of the data. Positional Encoding is then applied to extract structural, shape, or order features from the input. The Encoding stack, consisting of multiple layers with key components like Self-Attention and Multi-Head Attention, captures intricate features from the input. Finally, the Decoder, which has a similar structure to the encoder but serves a different purpose, generates outputs based on the features extracted by the encoder.
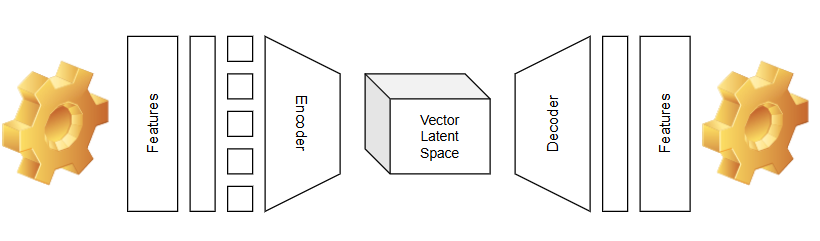
Have you noticed that Transformer models are all around us? If you use ChatGPT, Gemini Google AI, or Bing Copilot, you’re interacting with Transformer model architecture. This architecture is fundamental to both large language models (LLMs) and Generative AI models, enabling them to perform their impressive feats of understanding and creation.

Astraea Software Co., Ltd. a pioneer in 3D AI technology, has applied Transformer architecture to 3D applications. We use this architecture to build a generative AI synthesis model that creates new data by combining or synthesizing elements or features from existing data. for more detail about Synthesis Model AI see here, we also have a product of synthesis technology.
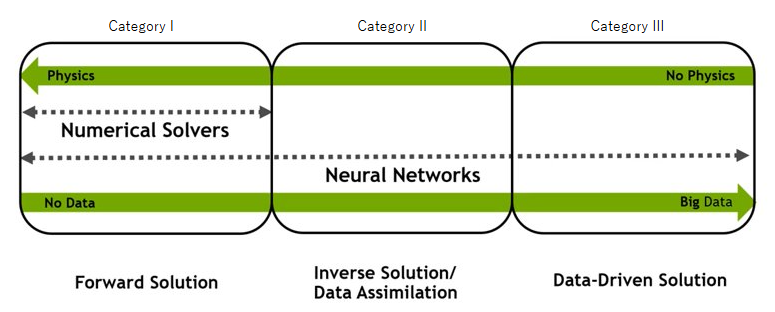
PINNs are a type of neural network that integrate physical laws directly into their architecture. This means they don’t just learn from data but also from the underlying physics governing the problem. Traditional AI models often function as “black boxes,” making it difficult to explain their choices or results. However, because PINNs incorporate physics equations, they produce results that adhere to physical constraints, making their outputs more interpretable and reliable within the boundaries of known physics.
Recently PINNs attract a lot of attention in engineering world, one of contributor of PINNs is NVIDIA with NVIDIA Modulus, an open-source framework designed to build, train, and fine-tune Physics-Informed Neural Networks (PINNs).
Beyond learning from data, PINNs uniquely incorporate physics equations directly into their loss function. (the thing they try to minimize during training), we used to call it data driven and physics driven. This enables them to operate in both data-rich and data-scarce environments. Even with limited or no data, PINNs can still produce reasonable solutions by trying to satisfy the embedded physics equations. The network learns by minimizing the error between its predictions and what the physics equations dictate.
Astraea Software Co., Ltd., a pioneer in 3D AI technology, is also at the forefront of research in Physics-Informed Neural Networks (PINNs) for 3D applications. Check out our detailed report [here]. Additionally, explore our demo page showcasing a simple 3D cantilever PINNs surrogate model.